Understanding Diffie-Hellman Key Exchange in Cryptography

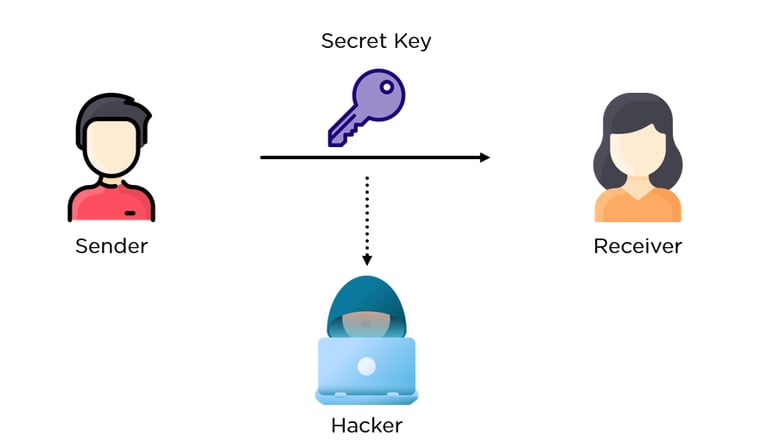
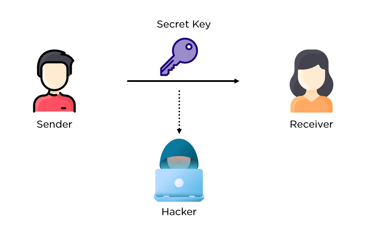
Diffie Hellman Key Exchange - How a Shared Secret is Created

Throughout the ages of human civilisation, encryption has been used for sensitive communication such as for military offensives, spy agencies and national security. The way in which this was done in the pre-internet era in the case of spy agencies is that the spy would meet up with their handler and they would physically share a "key" or secret with them. This would enable them to decrypt incoming communications as well as encrypt messages to be transmitted out securely to their handler

Within the age of the internet it would be highly inconvenient to have to meet up with every person you would like to securely communicate with online first to exchange a shared secret. This shared secret is essential to prevent man in the middle attacks, which is where person with malicious intent intercepts communication between the two communicating parties and can get ahold of sensitive financial information or other data. The Diffie Hellman Key Exchange method was created, which derived a shared secret between the two parties over an unsecure communication network. This method created the shared secret by sharing selective pieces of information which can be combined to derive the shared secret only by the two parties and not by any other parties who obtain these fragments of information shared over the unsecure network

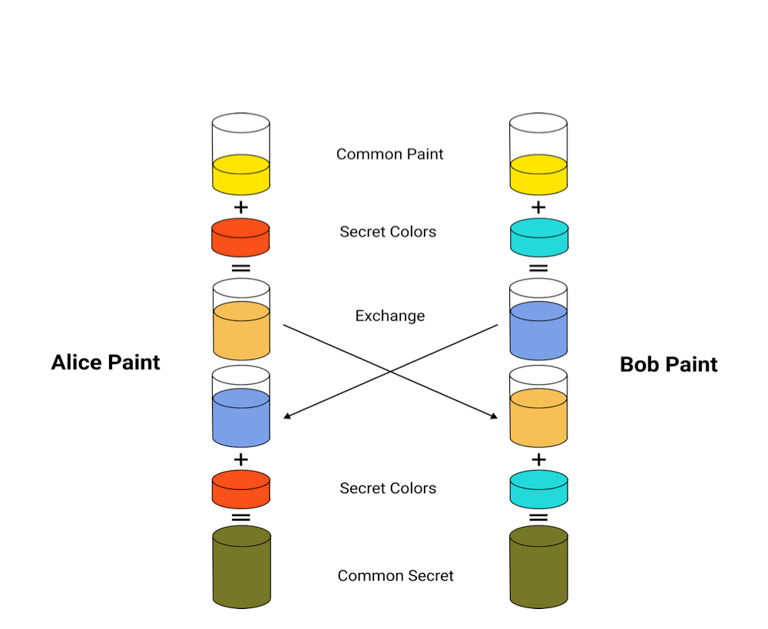
Shared Secret Paint Colour as an Analogy

Bob and Alice both have their own secret colours which are not shared. This secret colour is combined with a colour which is known by both and potentially observers (yellow in this case). These newly created colours with yellow and their own paint are exchanged between Alice and Bob, after the exchange they add their own colours in, arriving at a shared secret colour. This is simple to do in one way but in order to reverse this and try to determine the starting colours of Alice and Bob is theoretically possible but MUCH more difficult and impractical to do given what was publicly shared over the network. In cryptography the private paints represent the private keys of Alice and Bob, the common paint is a commonly known value, the exchanged paints are the public keys and the common secret allows both parties to securely communicate. This is the idea of the Diffie Hellman Key Exchange

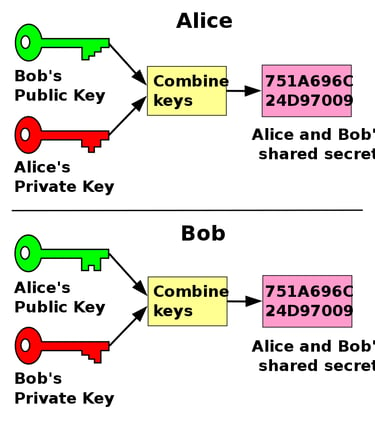
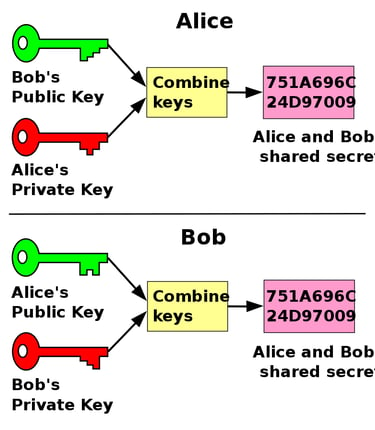
Cryptographic Keys to Generate a Shared Secret

Cryptographically, the way it works, is by both parties (Bob and Alice) generating their own secret keys. Bob and Alice both combine their keys with a known number (g) and they are shared publicly (The combination of this known quantity with their private keys yields their public key). Then Bob takes Alice's public key and vice versa to combine privately on their own machines with their own private key. The result after this final combination is an identical value where the combination created by both Bob and Alice are the same, without ever sharing this key over the communication network. This "symmetric key" which is a shared secret can encrypt and decrypt secure communications between the two parties. How is this done mathematically?

One Way Function - Easy to Do, Hard to Undo

One way functions enable public key cryptography. A one way function is computationally inexpensive in one direction, but trying to derive the starting value from the result takes many orders of magnitude more computing power. This an be compared to combining paint colours, simple and quick to combine the paint colours together, but extremely time and energy intensive to separate the colours, theoretically possible but not worth the time nor energy investment, we can see here how a shared secret is created.

Within public key cryptography, a shared secret is created using the discreet logarithm problem which is a useful and strong one way function which is useful for digital applications

It begins with a modulus function where we have:

The numerator which is an integer (i) and will be a primitive root, see below for explanation

This will be illustrated on a clock face with 17 as the modulus as 17 is a prime number

Let's imagine a clock face, but instead of 12 numbers, it has 17. We'll call this a "modulo 17 clock." 5 is a special number for this clock, called a "primitive root", the number 17 contains other primitive roots as well, but we will use 5. This means that if we start at 1 and keep multiplying by 5, wrapping around the clock face each time we go past 17, we'll eventually land on every number from 1 to 16 exactly once before returning to 1.

Think of it like this:

• 5¹ mod 17 = 5 (We start at 1, multiply by 5, and land on 5.)

• 5² mod 17 = 25 mod 17 = 8 (We multiply by 5 again, get 25. Since 25 is bigger than 17, we "wrap around" the clock face. 25 - 17 = 8, so we land on 8.)

• 5³ mod 17 = 125 mod 17 = 6 (Keep going, and we'll land on 6.)

If we keep going all the way up to 5¹⁶, we'll hit every number from 1 to 16. The prime number 17 is important because it guarantees we have primitive roots like 5 (and also 3, which is another one)

Now, imagine this clock is absolutely enormous, with a huge prime number of 'hours.' Someone tells you they've landed on the number 2,023,810 on this clock. You want to know what power of 5 they used to get there. This is an instance of the discrete logarithm problem. While trying every power of 5 one by one (brute-force) would eventually find the answer, it would be computationally very expensive and likely take an impractically long time for such a large number. Although brute-force is a solution, it's rarely the best solution. There are more sophisticated algorithms for tackling the discrete logarithm problem, but their efficiency varies depending on the specific prime number and other factors. The computational difficulty of solving discrete logarithms in large prime moduli is a crucial foundation for the security of many modern cryptographic systems

In essence, the Diffie-Hellman Key Exchange allows two parties to establish a shared secret key over an insecure channel. This is achieved through a clever mathematical dance involving one-way functions, specifically the discrete logarithm problem.

Imagine a giant clock face with a prime number of hours. One party chooses a secret number and "jumps" around the clock a certain number of times, landing on a specific hour. They publicly share this landing hour. The other party does the same, revealing their own landing hour.

Crucially, each party can then use their secret jump number and the other party's publicly shared landing hour to independently calculate the same secret meeting point on the clock. This shared meeting point becomes their encryption key, allowing them to securely communicate without ever exchanging it directly.

The beauty of Diffie-Hellman lies in the difficulty of reverse-engineering the original jump numbers from the publicly shared landing hours. This mathematical one-way street forms the bedrock of secure communication in today's digital world