Understanding Elliptic Curve Cryptography (ECC)

One of the fundamental underlying technologies of blockchain as well as many other internet technologies is a trapdoor function. The purpose of a trapdoor function is for a calculation to be able to be performed in one way quite simply such as multiplying 89 and 97, whereas going in the other direction and factoring this resultant product to find the two prime numbers which it consists of it will take much longer. This is utilised to generate an asymmetric key pair in which one is used for encryption which can be shared publicly and the other one is kept private for decryption. This technology was first available for use in 1976 utilising the Diffie-Hellman key exchange method which enabled asymmetric key algorithms.

Prior to public key cryptography, the receiver of the sensitive information would need a key or instructions on how to decode the message they were receiving, and if at any point this information was intercepted all messages sent using that encryption would be compromised

RSA cryptography was a common method developed by using principles from the Diffie-Hellman key exchange. It utilises prime number multiplication in order to generate a public/private key pair, whereas elliptic curve cryptography (which is used for bitcoin's digital signatures) utilises an elliptic curve to generate the key pair and can do so more efficiently than RSA requiring a smaller key size for the same level of security

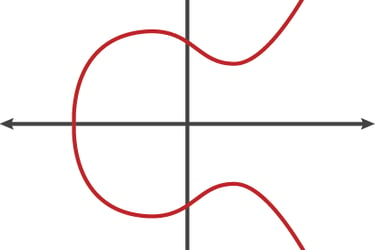
In order to generate an elliptic curve key pair, an elliptic curve is taken in the form y2 = x3 + Ax + B which will be the basis for generating our key pair

Two points are selected on our curve, one labelled 'A' and the other 'B'. A straight line is drawn between these points and as we can see there will be another point in which this line intersects the curve. A line is drawn directly down to the other side of the curve and a new line is created between our old point 'A' and this new point called 'C'. On the elliptical curve there will be another point of intersection. This process is repeated continuing to utilise point A for a mystery number of steps

Once a certain number of steps 'n' have been done as shown by the video above (could be billions of individual steps) an X and Y coordinate are generated. This coordinate could be 2.9234986592437659234875260348, 4.021394856913048650 for example. This is what becomes our public key and can be shared online. The private key is the number of steps it took us to get from step one to this coordinate for example it could be 1089236498234193845. So we are able to share the graph in which we generated our key, and the final X and Y coordinate which makes the private and public key linked, the amount of computing power to find the number of steps by just knowing the final coordinate would require impractical amounts of computing power over large time scales making this form of cryptography secure and practical