Merkle Trees in Cryptographic Architecture

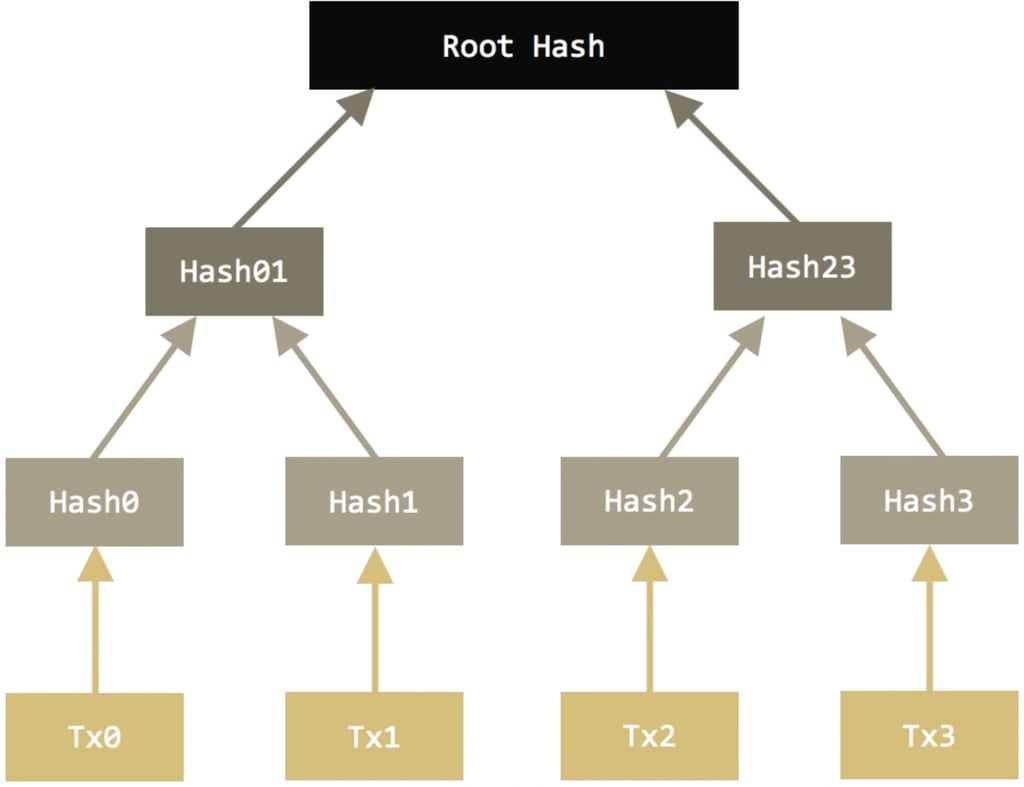
Utility of Merkle Trees

Merkle Trees play a key role in cryptocurrencies as they allow for compression in data storage, providing a key fingerprint (root hash) of massive amounts of data in a single cryptographic hash of size analogous to any other hash which can be used to verify if certain pieces of data are apart of the root hash to determine authenticity of the data in a quick methodical way. Merkle trees have many digital applications such as peer-to-peer file sharing, where the data may be downloaded from differing sources for each portion of the whole file. The data of the entire file can be embedded within a Merkle tree to ensure its validity and that it has not been tampered with when bits and pieces are downloaded from each peer. The client which downloads files can easily verify the piece of data and check that it is apart of the merkle root to ensure validity and that the data has not been tampered with. Merkle trees are used across the cryptocurrency field in differing ways suited to the goals of each blockchain. Ethereum and Monero both use modified Merkle trees in order to accomplish their desired outcomes

Hashing Algorithm Overview

Hashing algorithms take some file or data and pass it through a function in order to get an output of uniform length. This output is the fingerprint of the original data which within the SHA-256 algorithm used for bitcoin has a maximum input size of 2.1 billion GB, and a small 256 bit output which can be represented in different ways such as ones and zeros or the commonly used hexadecimal format of numbers 1-9 and letters a-f looking something like the following

5e884898da28047151d0e56f8dc6292773603d0d6aabbdd62a11ef721d1542d8

This tiny amount of output can be used as a fingerprint for very large files, providing an easy way to check the validity of files in a simple way.

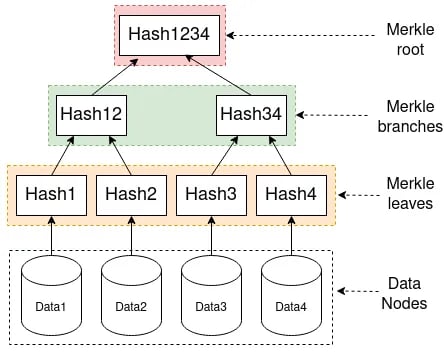
Creating the Merkle Root

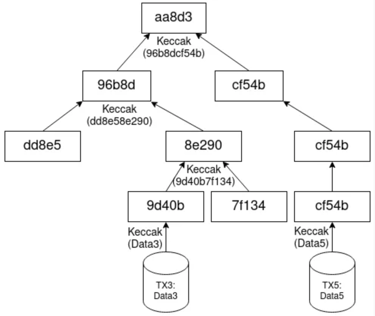
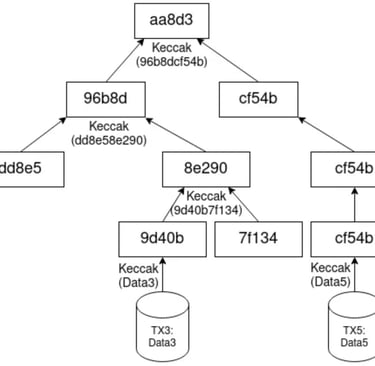
The Merkle root is created by hashing data in the same way as seen above. The hashes of the data are then paired up and combined or concatenated, then they are rehashed in order to create a new hash of the paired data. This step is then repeated until there is a single hash which is a combination of all of all of the inputted providing a fingerprint of all of the data in a single hash function in a hierarchical set of data. In order to determine if Data 2 is apart of the Merkle tree, we would require Hash 1, and Hash 34 only and not the other hashes. We would hash Data one to produce Hash 1, then concatenate it with Hash 2 and rehash, we would then take this Hash we have created (Hash 12) and combine and rehash with the provided Hash 34 and if the resulting hash is the same as the provided Merkle root hash, we could then be certain that Data 2 is in fact apart of this Merkle tree function, if a different root function is obtained, then we will know that Data 2 is in fact not apart of this Merkle tree

This gives an easy way to verify through a series of branches as opposed to checking every piece of data and resulting hash. The scaling is logarithmic, so if there are 1024 pieces of data, in order to check the Merkle root consists of one specific piece of data, there would be 10 levels within the tree (2^10 = 1024), so we would only need to check 10 sets of hashes in order to determine if our data is in fact apart of the Merkle Root and confirm the validity, which is much more efficient than if we were to just hash all the data together, then all of the 1024 data inputs would need to be checked

How Merkle Enables More Efficient Blockchain

Within each Bitcoin block, there is a block header. The block header is a digital fingerprint of the block which contains information pertaining to the transactions of the block as well as a digital footprint of the previous block as well as some other information such as the timestamp and other less relevant information

Importantly, the block header contains the previous block hash which is the SHA-256 hash of the parent block's header as well as the Merkle root which is the final hash of the block's transactions, the root of the merkle tree. In order to find a proof of work, miners will hash the block header over and over again until they find an applicable proof of work solution which contains a certain amount of zeros at the start and that number depends on the current difficulty setting which on average will take 10 minutes with the hashing power on the network at any given time

The thing which allows each bitcoin block to be linked to the next in an immutable way is the fingerprint of the parent block included in the block header which is hashed in combination with the other relevant information in order to create the block header. The merkle tree allows the transactions that are included in a block to be able to be verified without having to go through each transaction which is scaled logarithmically increasing efficiency

Pruning The Merkle Tree

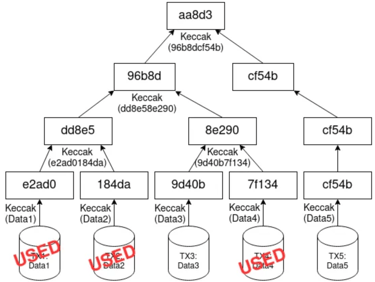
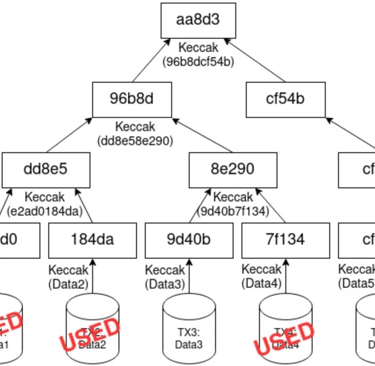
Bitcoin relies on the UTXO or unspent transaction output model, unlike Ethereum which is user account based. When a bitcoin transaction is conducted, for example Bob has 0.5 BTC in his wallet and decides to send 0.3 BTC to Alice. 0.3 BTC gets sent to Alice and 0.2 BTC gets returned to Bob under a brand new UTXO as change. The previous UTXO which had contained the 0.5 BTC is marked as spend

In order to conserve blockchain space for lightweight nodes, pruning of the merkle tree which contains the transactions can be done while still conserving the same root hash value, thus conserving the efficacy of the blockchain

On the left, we have a merkle tree of an example of transactions within a bitcoin block, and the coalescing of the hashes down into a root hash function. On the right, some of the used transaction outputs can be pruned off the tree in order to save blockspace

Conclusion: The power and versitility of merkle trees

Merkle Trees stand as one of the most elegant and efficient cryptographic structures in modern computing, with their influence extending far beyond Bitcoin. By compressing vast amounts of data into a single, verifiable fingerprint (the Merkle Root), they enable secure and scalable validation without requiring full data replication. This logarithmic efficiency is revolutionary—whether in blockchain networks, peer-to-peer file sharing, or even version control systems like Git.

In Bitcoin, Merkle Trees serve as the backbone of transaction verification, allowing lightweight nodes to confirm data integrity without storing the entire blockchain. Their hierarchical hashing structure ensures tamper-proof records while optimizing storage through pruning—essential for maintaining a decentralized yet efficient network. Beyond Bitcoin, variations of Merkle Trees (like Ethereum’s Patricia Tries) adapt the concept to suit different consensus models, proving its flexibility.

The true brilliance of Merkle Trees lies in their simplicity: a cryptographic tool that scales seamlessly, balances security with performance, and underpins trust in decentralized systems. As blockchain technology evolves, Merkle Trees will remain foundational—whether in optimizing existing networks or enabling new innovations in distributed computing.

For developers, investors, and enthusiasts alike, understanding Merkle Trees isn’t just academic—it’s key to grasping how trustless systems actually work. From verifying a single transaction to securing entire networks, their utility is a testament to the power of clever cryptography.

Teemu Kanstrén